前面幾天提到過,當一個模型的參數較多,會導致模型複雜度過高,這會讓模型在訓練資料的擬和表現很好,但在新的陌生資料上 ( 測試資料 ) 表現不佳,就會出現過度擬和的情況,對於過度擬和的問題,我們就可以透過正則化的技術來降低模型的複雜性,確保模型的效能不會過度擬和,以提高模型的泛化能力,通常正則化會用到的方法有權重正則化、彈性網路 ( Elastic Net )、早停 ( Early Stopping )、丟棄 ( Dropout )。
權重的正則化指的就是在模型的損失函數後面再加上一項 ,這個
能夠在梯度下降做參數 ( 權重 ) 更新的時候防止權重過大,能夠減小權重的大小或者讓權重為 0,以避免模型過度擬和,對於權重的正則化有兩種方式,一種是 L1 正則化 ( Lasso Regularization ),一種是 L2 正則化 ( Ridge Regularization ),和彈性網路正則化 ( Elastic Net Regularization )。
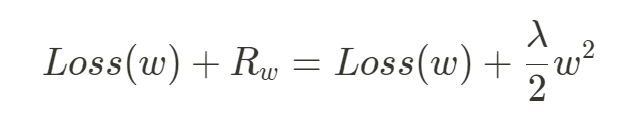
在做 L2 正則化時懲罰項 ,
為一個超參數,控制正則項影響整個損失函數的比重 ( 懲罰的程度 ),該值越大,正則項的作用 ( 縮小權重 ) 就越大,越能夠防止過度擬和;該值越小,正則項的作用越小,防止過度擬和的能力較弱,在上面公式把
再除以 2 是為了之後方便求梯度,在做參數更新時,會求損失函數對參數的梯度,如下:
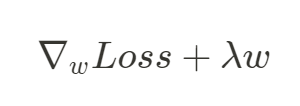
在參數 更新時,
為學習率:
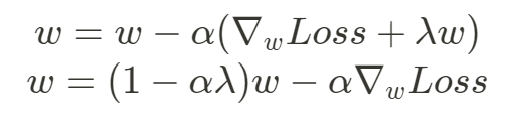
上面公式中可以發現當 越大 ( 大於 0 ),就越能夠有效減小
權重,
越接近 0 的話,
的減小效果就越弱,
= 0 時
大小則不會改變,即不使用正則化, 整個 L2 正則化的過程中,權重逐漸趨向更小的值、更接近 0 的值,目標就是使模型的權重變得很小,但不會完全縮小至 0,針對這點有助於減少不同特徵之間的差異,提高模型的穩定性。
L1 正則化的功能和 L2 相似,一樣會在損失函數後面加上懲罰項 去減小權重的大小,只是兩種正則化方式的懲罰項 ( 正則項 ) 長得不一樣,如下:
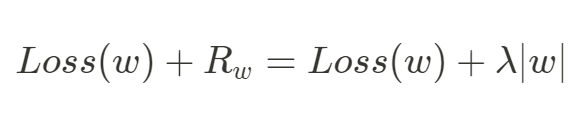
做 L1 正則化時懲罰項 ,在參數更新時需要計算損失函數對於參數的梯度,會對懲罰項
求梯度 ,也就是對絕對值函數
求導數,如下:
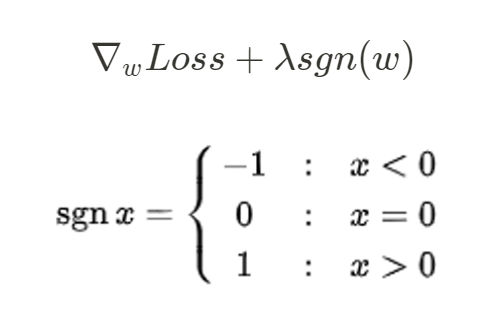
在下面參數更新時,就會發現到 L1 正則化和 L2 正則化對於權重的影響略有不同,L2 會使所有的權值 減小,縮小後的值仍和縮小前保持同號,但 L1 正則化時,當
時,更新權重的時候會讓權重減小,當
時,更新權種會讓權重變大,這就意味梯度優化時, L1 會激勵著權重
往 0 的地方接近或者為 0,使得最後的權重變得較稀疏,也就是所有權種中只有少數權重不為 0,假設現在有多個特徵,但是只有少數的特徵對結果較有影響,這是就可利用 L1 將權重設為 0 的特性將一些不重要的特徵忽略,實現了對特徵的選擇,並達到減小模型複雜度的目的,這裡就是和 L2 主要不同的地方。
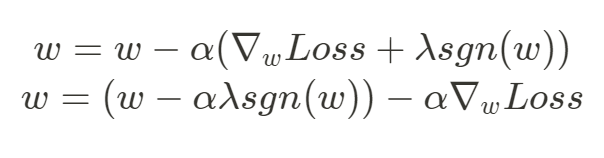
兩個正則化方法的懲罰項長相都不同,L2 是引入權重平方,而 L1 是引用權重的絕對值,這樣與損失函數結合後的結果會在梯度優化做正則化時,讓 L2 專注在減小權重的大小,但不會減小至 0,目的為了讓彼此間特徵的差距不要過大,但不會去忽略特徵,但換是 L1,就會專注在讓權重變得稀疏、促使權重減小至 0 甚至為 0, 因此 L1 會比 L2 導致更稀疏的權重,因為 L1 有著能夠讓權重為 0 的特性,就可用來做特徵的選擇,將一些不重要的特徵權重設為 0,僅留下重要的特徵,以上就是兩個正則化方式的大致差異。
彈性網路正則化,其正則項 ,意味著它結合了 L1 正則化對權重的減小與 L2 正則化對特徵選擇的優點,有效減小過度擬和的發生和提高模型的泛化能力。
Dropout 也是一種用來正則化神經網路的方法,目標就是要減少過度擬和的情況,Dropout 就是在模型訓練時在神經網路中刪去、關閉 ( Drop out ) 掉一些神經元,至於如何實現,就是將該層的輸出設置為 0,也就是說會控制神經元的啟動或關閉狀態。
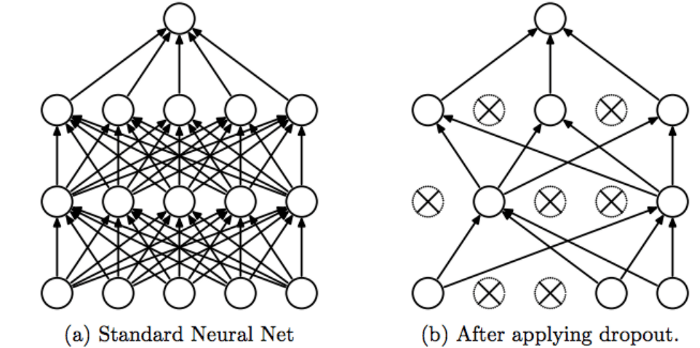
我們知道每一層神經元的權重都會乘以上一層神經元的輸出,如上圖 a,這是我們一般沒有使用 Dropout 的神經網路,每層的神經元輸出都會被啟動,所以層與層之間神經元的依賴性會較高,至於在上圖 b 的部分,它是有採用 Dropout 機制的神經網路,它控制了每層中神經元的啟動或關閉狀態,只要神經元被關閉,它的輸出就會為零,傳到下層的神經元與權重相乘時結果就會為 0,對於下層神經元,意味者對於來自上層神經元輸出至這層的特徵輸入可以省略,也就是與這層的神經元斷開連結,所以上圖 b 中那些被關閉的神經元會被打叉,其連結到下層神經元的箭頭也連帶被刪去。
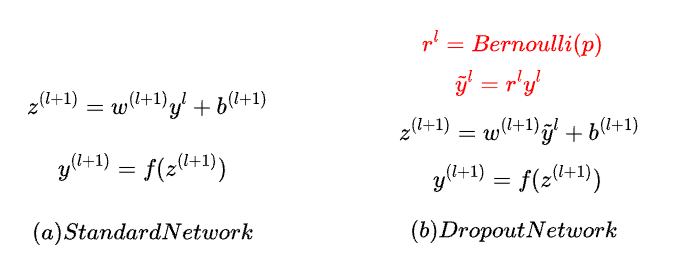
上圖 a 就是一般神經網路( 沒有用 Dropout ) 的每層的輸出函數,就是把權重 乘以上層的輸出,當我們的神經網路使用 Dropout 時,會針對每層的輸出中,把每個輸出值再乘上一個
,Dropout 會在每層中,依據 Bernoulli Distribution 以機率 p 生成 0,也就是神經元關閉的機率,再以機率 ( 1 - p ) 生成 1,也就是神經元啟動的機率 ( 存活率 ),這些生成的 0 和 1,就是
中的元素,會拿來一個個與當前層中的神經元輸出做相乘,就可以控制每層中的神經元要有幾個啟動幾個關閉,像是當前的隱藏層中有 1000 個神經元,Dropout 的機率 p 為 0.5,
中 0 和 1 數量各半,表示有 500 個神經元會被關閉,500 個會被啟動,最後再根據機率隨機選擇神經元做關閉和啟動,不同的層中可有不同的存活率,通常較靠近輸入層的層會用較高的存活率,較深的層 ( 靠近輸出層 ) 會用較低的存活率,以加強正則化的效果。
這邊我們用到 Ensemble Learning 的概念,就是我們模型最終的輸出結果,會是先前考慮多個不同模型的結果之平均,有點像是多數決的概念,不會因為過度依賴少數人而產生偏見,而 Dropout 用的概念也相似,透過讓某些神經元處於關閉和啟動狀態,最後會輸出神經網路函數,在做梯度下降訓練時,每次的迭代都會藉由 Dropout 機制隨機使某些神經元關閉或啟動,因此每此迭代最後所產生的神經網路函數都不相同,也就是說對於我們最終訓練得出的神經網路函數,會是經過綜合平均每次迭代得到的輸出函數所得到的結果,就像是有許多人投票而非只有少數人,最後可以得到能夠代表多數人想法的結果,有效的避免過度擬和。
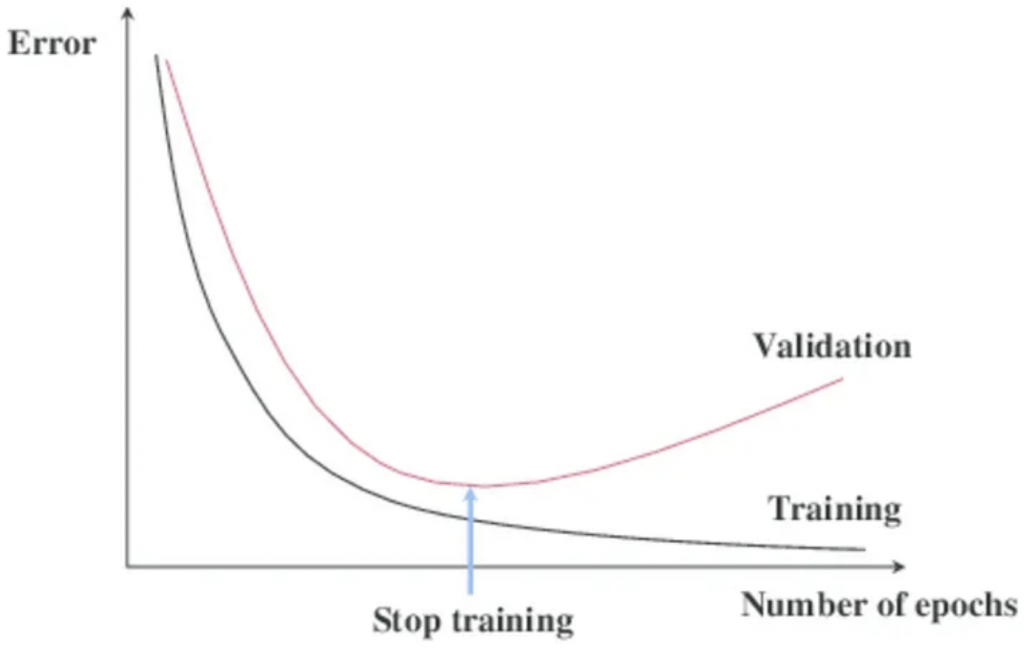
早停 ( Early Stopping ) 也是用來防止模型過度擬和常用的方式,主要的概念就是在模型的訓練時的每次迭代中,檢測其在驗證集的表現,發現模型在驗證集上的錯誤率開始上升,就停止整個訓練過程,能夠避免模型再繼續訓練下去而導致過度擬和的情況,使模型泛化能力降低。
今天我們學到:
我們下篇文章見 ~
https://blog.csdn.net/xpy870663266/article/details/104573194
https://datasciocean.tech/deep-learning-core-concept/understand-dropout-in-deep-learning/
